垂直・平行と四角形 いろいろな四角形① 絵地図の道を直線で表しました。その地図の中で、台形と平行四辺形 は、どれですか。台形は赤で、平行四辺形は青でぬりましょう。 下の(ア)と(イ)の直線は、平行です。これを使って、台形を1つ、平行四辺平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角・ひし形の面積 対角線の長さからひし形の面積を計算します。 ・平行四辺形の面積(底辺と高さ) 底辺と高さから平行四辺形の面積を計算します。 ・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。

数学角度 高校入試レベルの意外と悩んでしまう平行四辺形の良問 Youtube
平行四辺形 対角線 角度
平行四辺形 対角線 角度- 正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 (二等辺三角形に分ける方法については、計算問題①で解説します!) 正 n 角形の面積の公式(n = 3, 4, 5, 6)学習のポイント 垂直・平行や台形・平行四辺形・ひし形の性質や、そのかき方を学習します。対角線の特徴に着目して、四角形の性質をとらえるように理解しましょう。 角の大きさに着目して、直線の交わり方について考えましょう。 垂直



4年算数 垂直 平行と四角形 2 教え方
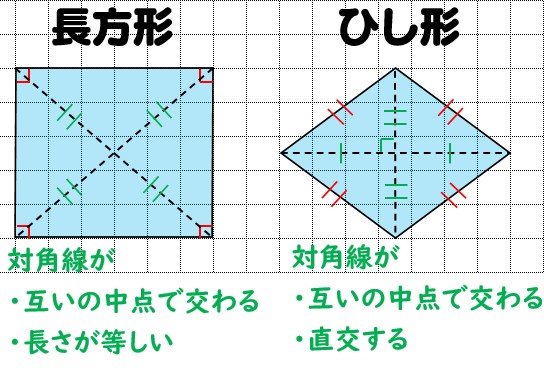
になってるからね。 Step3 三平方の定理で立方体の対角線を求める 次は 立方体の対角線 を求めていくよ。 さっき見つけた直角三角形で三平方の定理を使えばいいのさ。図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する
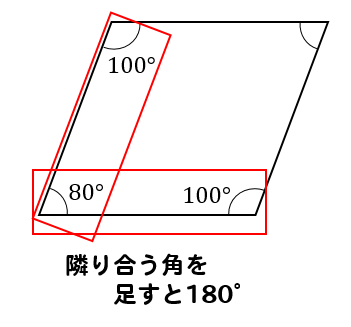
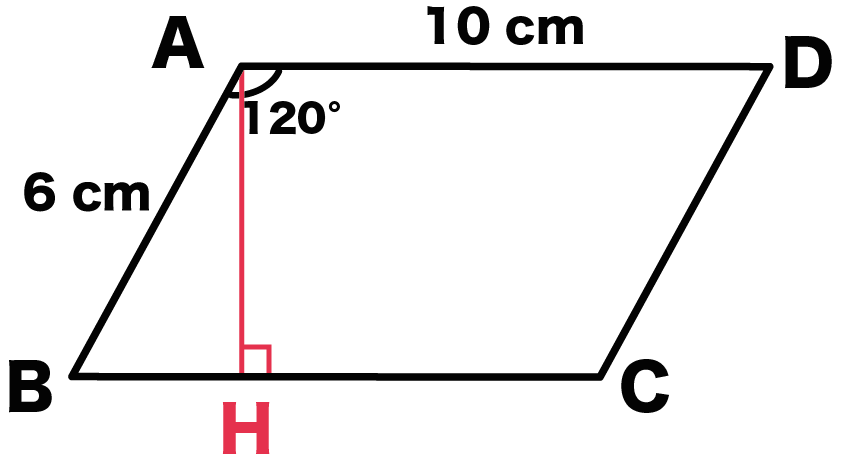
平行四辺形abcdのab = 6 cm、角a = 1°だとしよう。 まず、 角度がわかっている頂点から垂線をおろす。 向かい側の辺にね。 平行四辺形abcdでいうと、 aからbcに垂線をおろすよ。 交点をhとしよう。 平行四辺形の2組の向かいあう角はそれぞれ等しいから、 角a三角形 square 正方形 rectangle 長方形 diamond / rhombus ひし形 parallelogram 平行四辺形 trapezium / trapezoid 台形 次に図形の部位を表現する英単語です。 corner とがった角 angle 角、角度 side 辺 plane 面 right angle 直角(90度) diagonals 対角線、斜線 2「立体図形」の正方形の面積の公式、対角線による求め方 正方形の面積の公式を下記に示します。 A= a 2 Aは正方形の面積、aは辺の長さです。皆さんご存知の公式ですが、実は、正方形の辺の長さでは無く「対角線の長さ」から求めることが可能です。 下図をみてください。
対角線上に並ぶ小立方体は、1つの対角線で3個 したがって、合計は3個×4(対角線の数)=12個から、 各対角線が共有する中央の1個を3個分引き、 12- 3 =9で、9個になります。 1辺が4個でできている場合(図2)には、「平行四辺形がひし形になる条件」と同じです。 ~ひし形が正方形になる条件~ ・対角線の長さが等しいひし形は正方形です。 ・一つでも直角があるひし形は正方形です。 「平行四辺形が長方形になる条件」と同じです。平行四辺形を二等分するためには 対角線の交点を通るように直線をひけば良かったですね。 ということで まずは、平行四辺形の対角線の交点の座標を求めます。
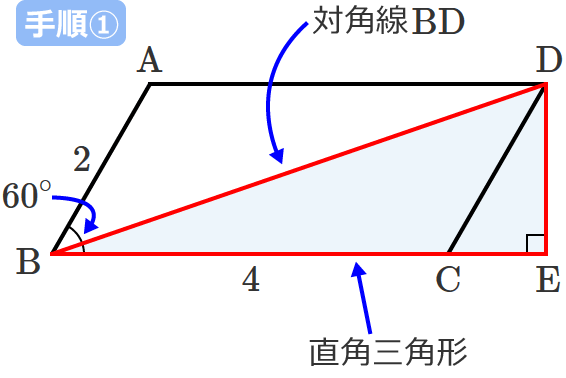



平行四辺形の対角線の長さの求め方
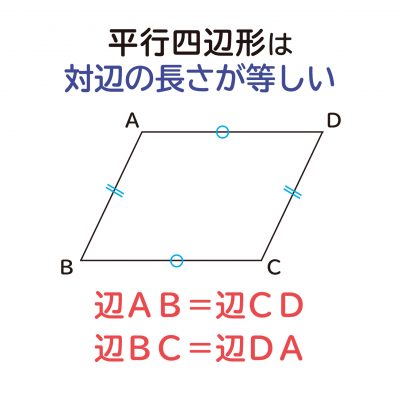



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル
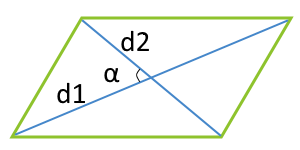
平行四辺形の面積を対角線の長さと角度から求める $2$ つの対角線の長さが $4$ , $6$ 、その2辺のなす角が $60°$ のとき、その平行四辺形の面積を求めよ 対角線は他の対角線の中点で交わるってことを利用して、図にするとこうなるね平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基




ボード 勉強 のピン



平行四辺形 対角線 長さ 計算
では平行四辺形の性質を定義から証明してみましょう。 平行四辺形の性質の証明 平行四辺形の定義を仮定したとき、それぞれの性質をもつことを証明しましょう。 四角形abcdにおいて対角線の交点ひし形と正方形、平行四辺形との違い ひし形、正方形、平行四辺形の違いを下記に示します。 ひし形 ⇒ 全ての辺の長さが等しい四角形 平行四辺形 ⇒ 2組の辺の長さ等しい四角形 正方形 ⇒ 全ての辺の長さ・角度が等しい四角形 ひし形と対角線の関係2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。



第175問の解答




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
☆まいにち一題☆ 中学受験過去問題研究本ブログでは、中学受験を目指す方、興味を お持ちの方を対象に『解き応えのある問題』や 『基本・応用を身に付けるにふさわしい問題』を 5段階の難易度に分け、わかりやすく解説して おります こんにちは、ウチダショウマです。 今日は、中学2年生で扱う 「等積変形」 について、特に台形と等しい面積の三角形を作る方法を解説していきます。 また、等積変形の基本 $2$ つを押さえたうえで、一緒に応用問題(難問)にチャレンジしてみましょう♪ 等積変形の基本2つ 等積変形とは平面図形 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める
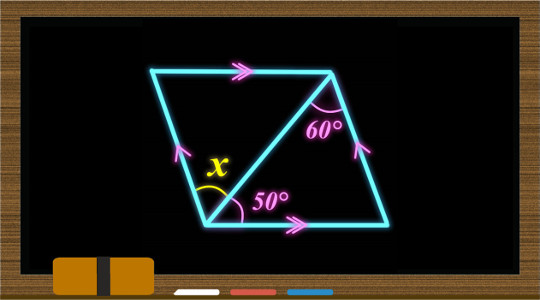



毎日脳トレ Xの角度はいくつ 平行四辺形の法則がわかれば解ける Dアプリ レビュー




数学角度 高校入試レベルの意外と悩んでしまう平行四辺形の良問 Youtube
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。すなわち平行四辺形の対角線が合力となります。 もし 2つの力の角度が1°であるなら この青い三角形は正三角形であり、平行四辺形の対角線の長さは各辺の長さと同じになるので、 合力は 2n となります。2n + 2n が 2n となるのです。4n とはなりません。



平行四辺形と角度 中学から数学だいすき
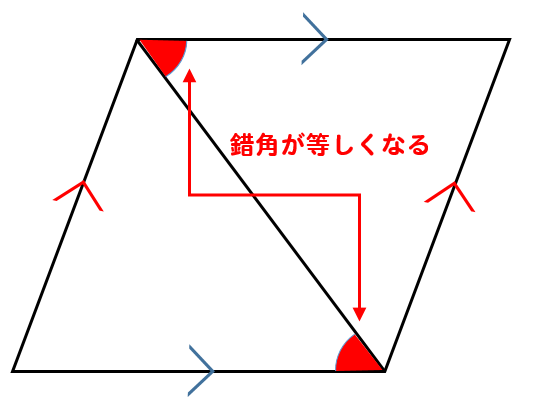



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



Happylilac Net 4nen Sikakukei Ans Pdf
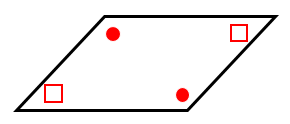



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
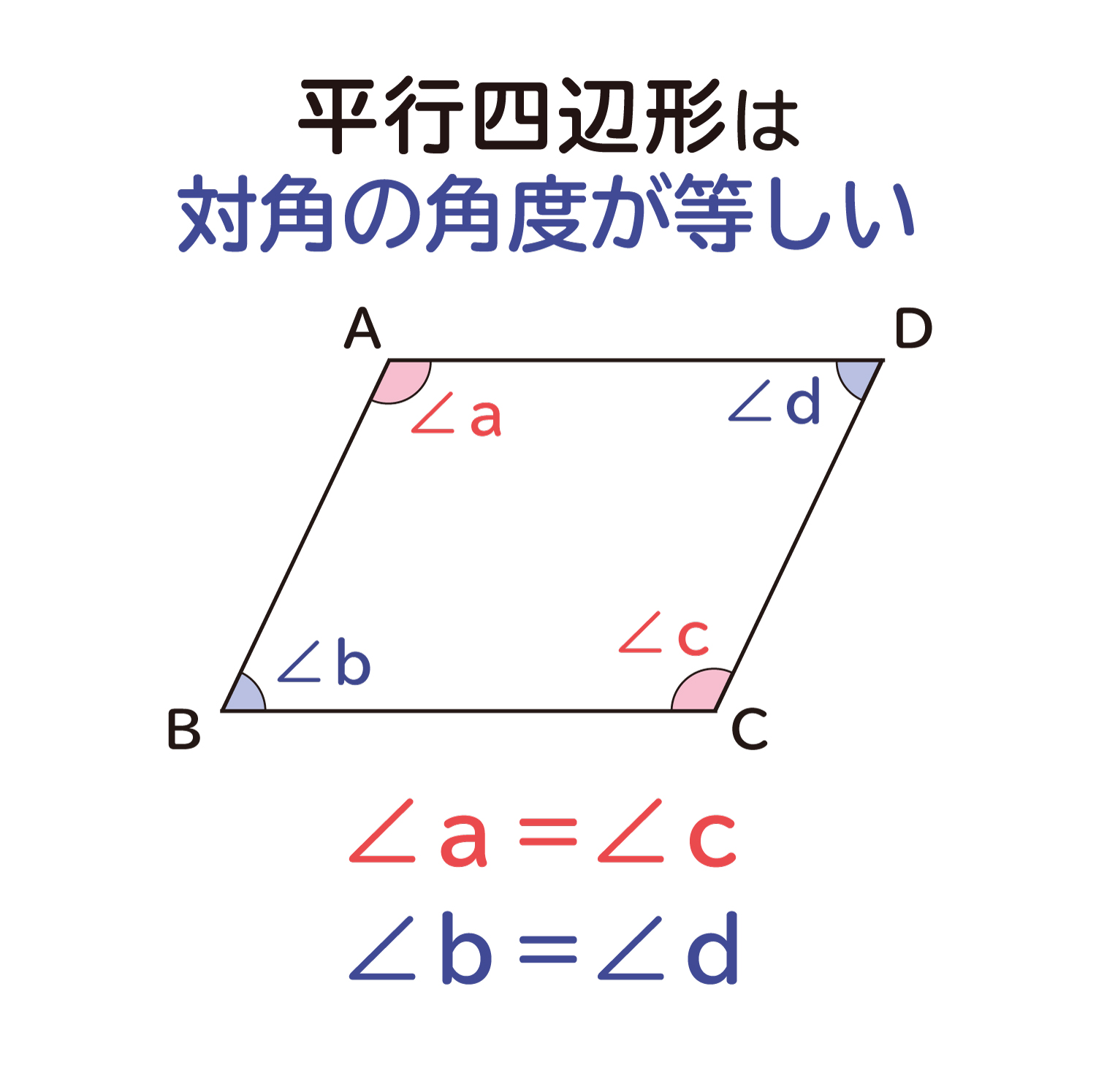



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




中2数学 平行四辺形の性質 練習編 映像授業のtry It トライイット




平行四辺形で知っておくべきこと 苦手な数学を簡単に



Math 平行四辺形 平行四辺形になることの証明 働きアリ
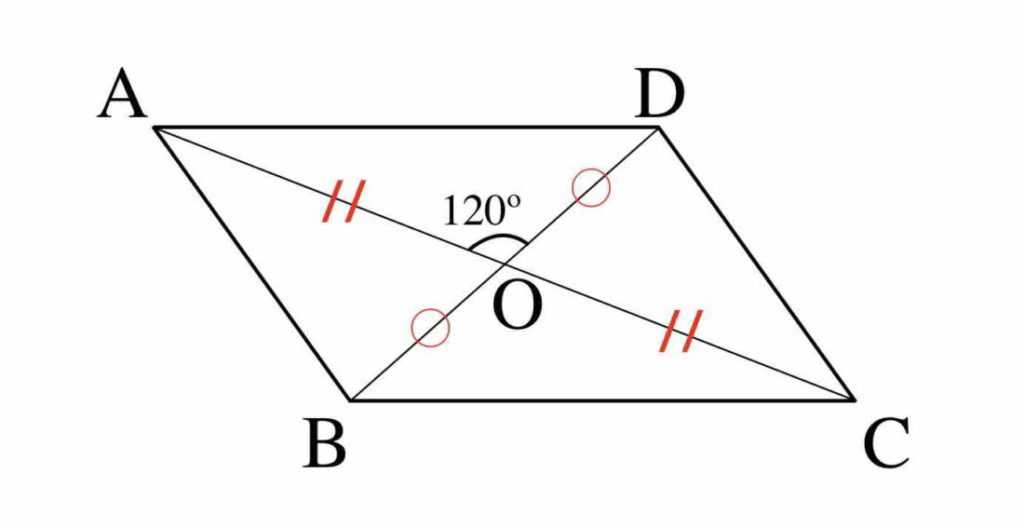



三角比を用いた面積計算をマスターしよう スタディクラブ情報局




平行四辺形の辺や角を求める Youtube




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
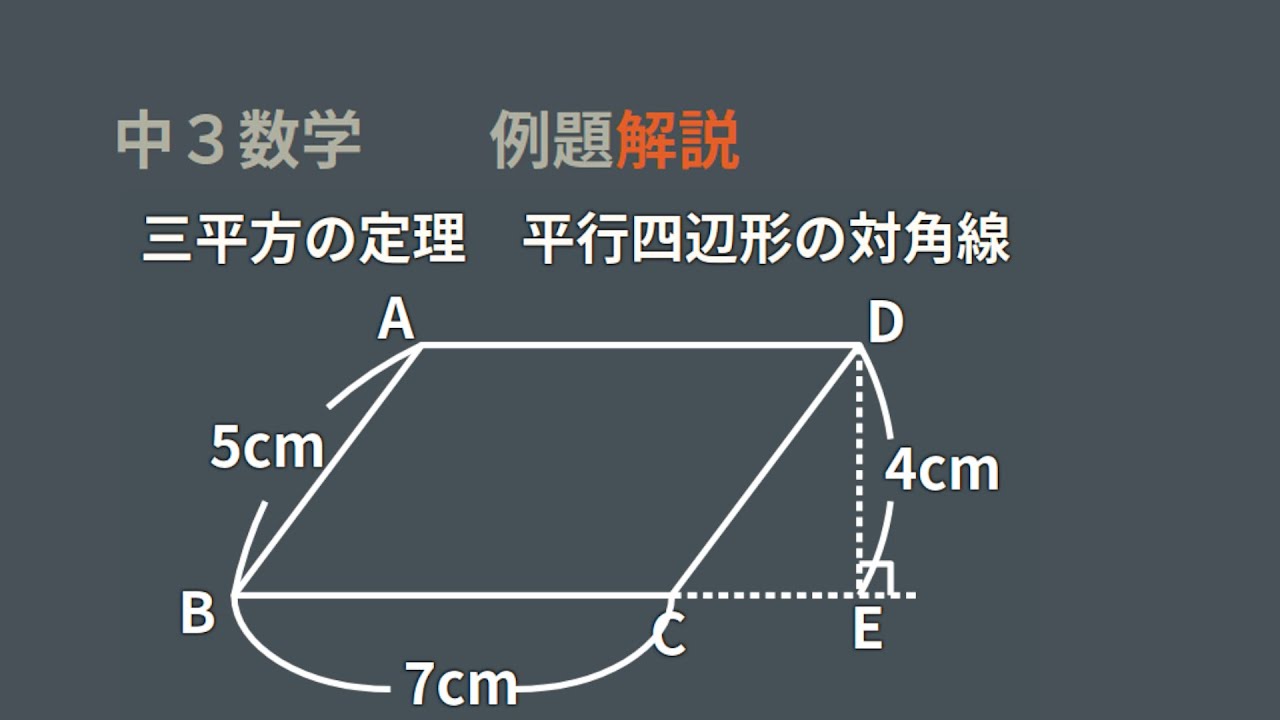



三平方の定理 平行四辺形の対角線




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
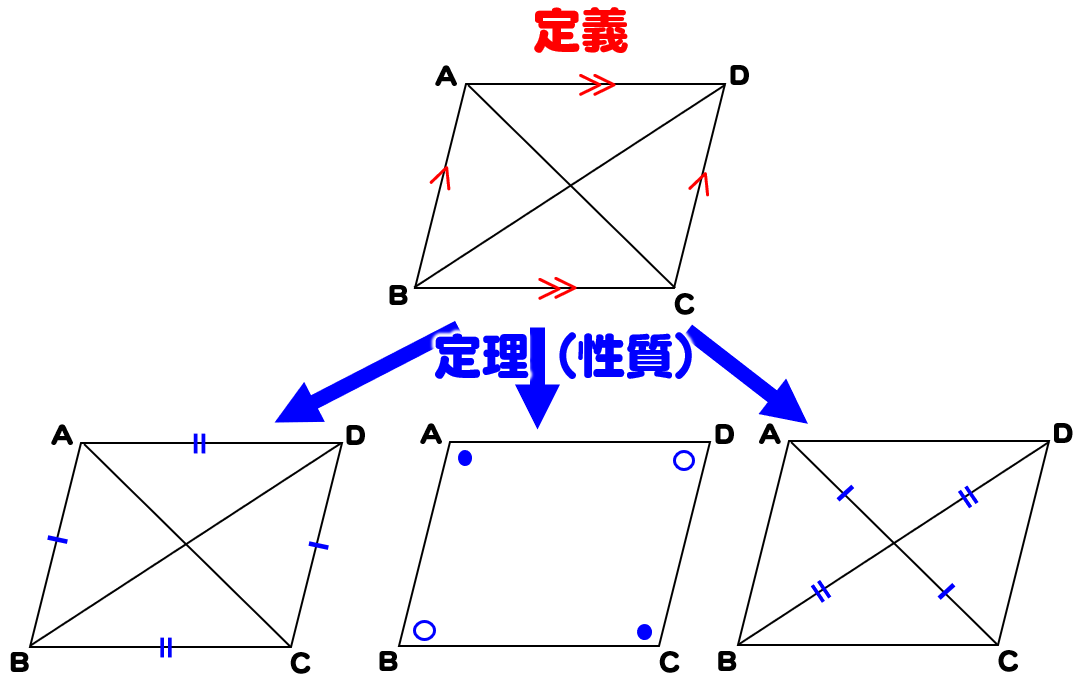



平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形 対角線 長さ 計算
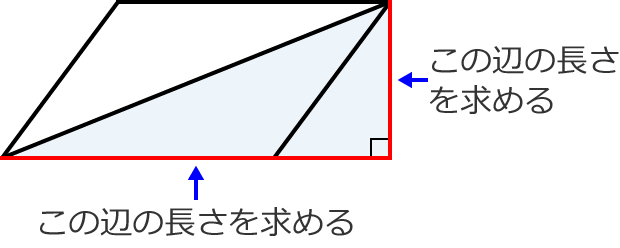



平行四辺形の対角線の長さの求め方
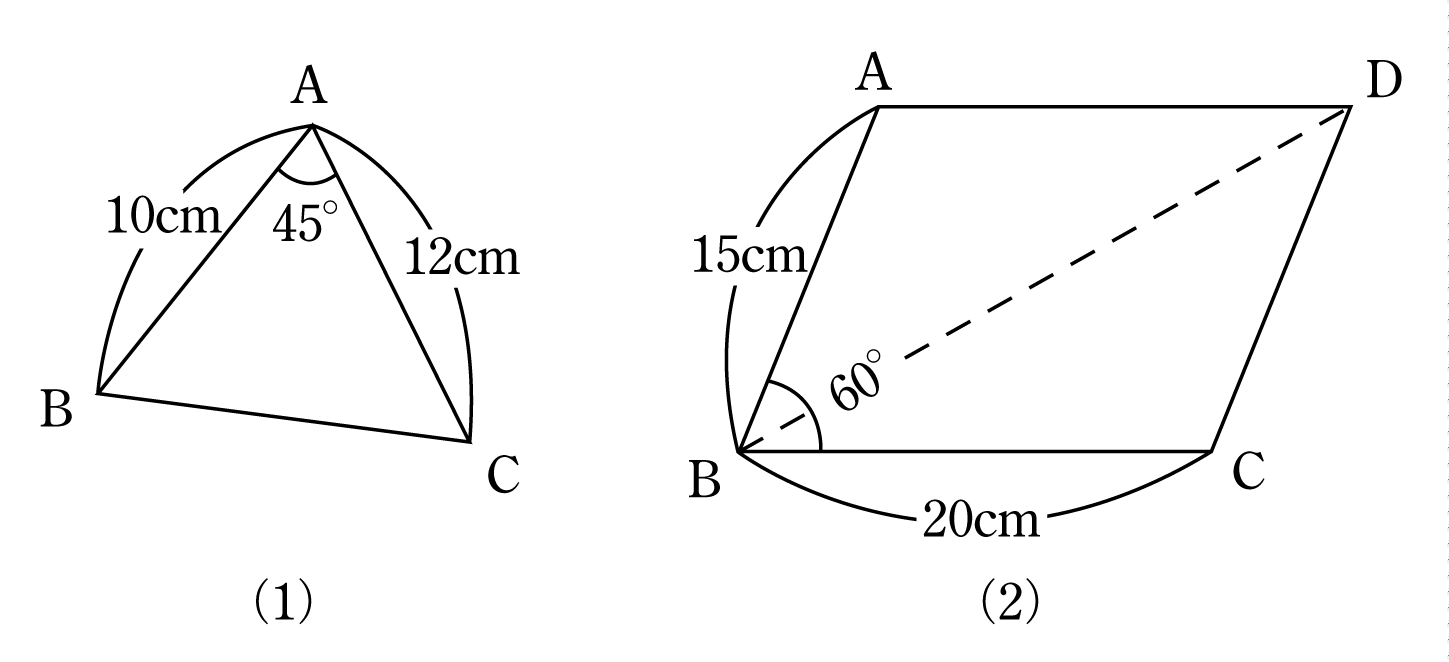



平行四辺形 対角線 長さ 計算




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
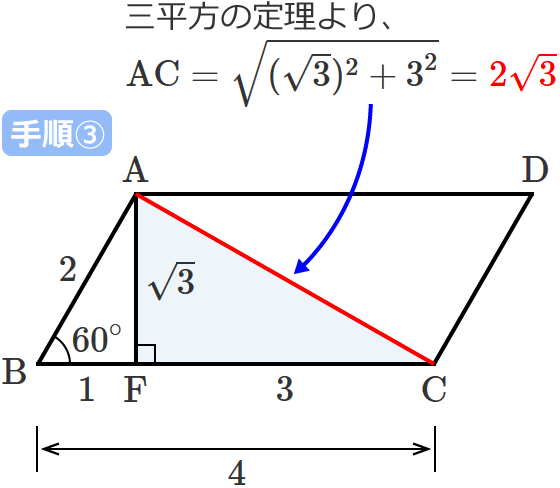



平行四辺形の対角線の長さの求め方




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



4年算数 垂直 平行と四角形 2 教え方




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



4年算数 垂直 平行と四角形 2 教え方




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方
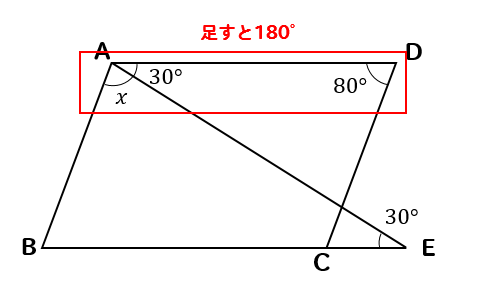



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
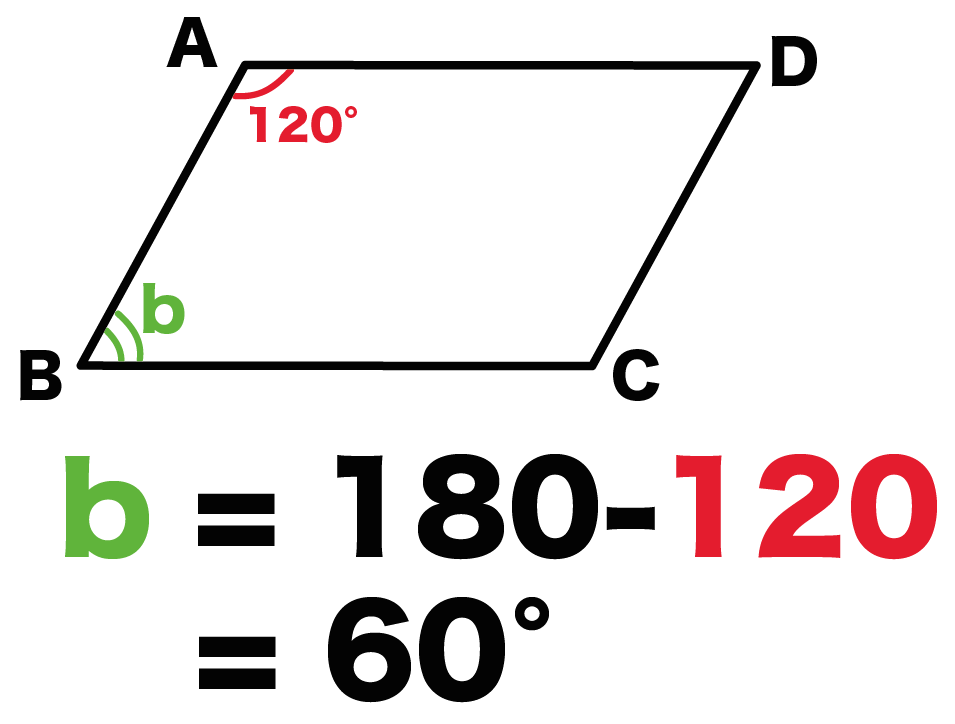



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



平行四辺形の角の二等分線



平行四辺形の対角線で分けられた角は 2等分されている やばいです Yahoo 知恵袋



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



1



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




テストの問題なのですが 青で丸をつけた所の角度が分からないので答えはもらったので分か Clear




平行四辺形について知ろう 苦手な数学を簡単に
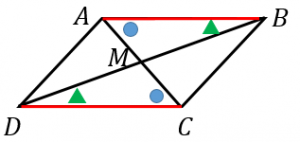



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



平行四辺形abcdについてcabの角度求め方を教えて下さい Yahoo 知恵袋




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント




平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo



平行四辺形の性質の証明
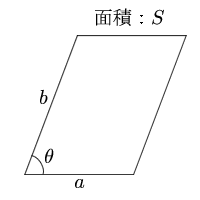



平行四辺形 2辺と間の角度 面積の計算 計算サイト



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形について知ろう 苦手な数学を簡単に



平行四辺形の対角線の角度について この条件の時の角度a Bを文字で表 Yahoo 知恵袋



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




平行四辺形の対角線の長さの求め方



平行四辺形の面積




鈍角の角の頂点から引き出される平行四辺形の高さは方向に等しい 半分に分けます 平行四辺形の急性の角度は 30 度です 平行四辺形の対角線を見つけます のイラスト素材 ベクタ Image 0312



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
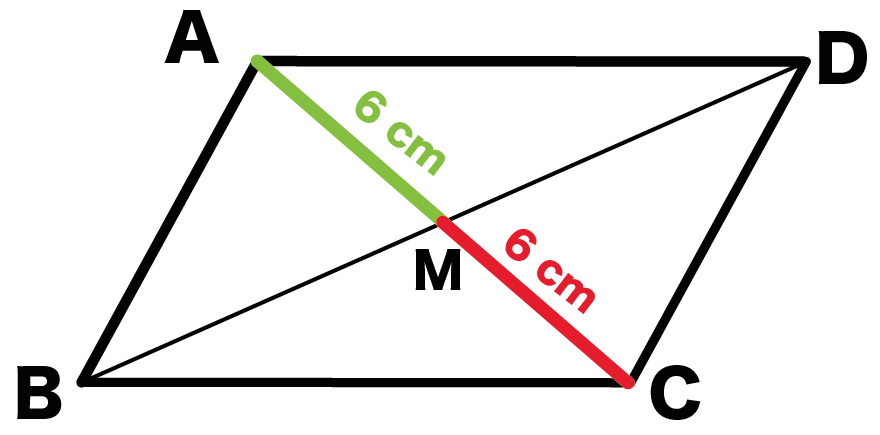



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の対角線の長さの求め方



角を求める問題
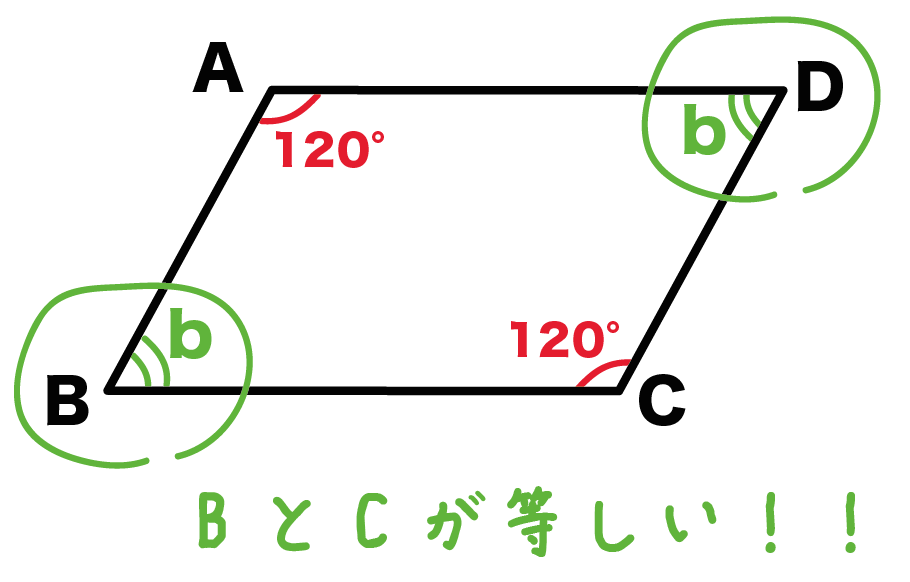



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




小5算数 平行四辺形が描けると 角の大きさがわかる ブログ アビット




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
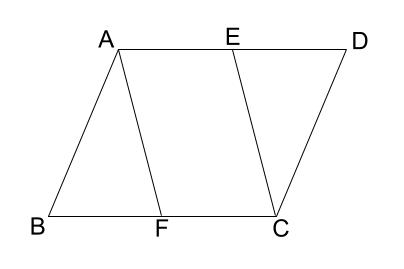



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
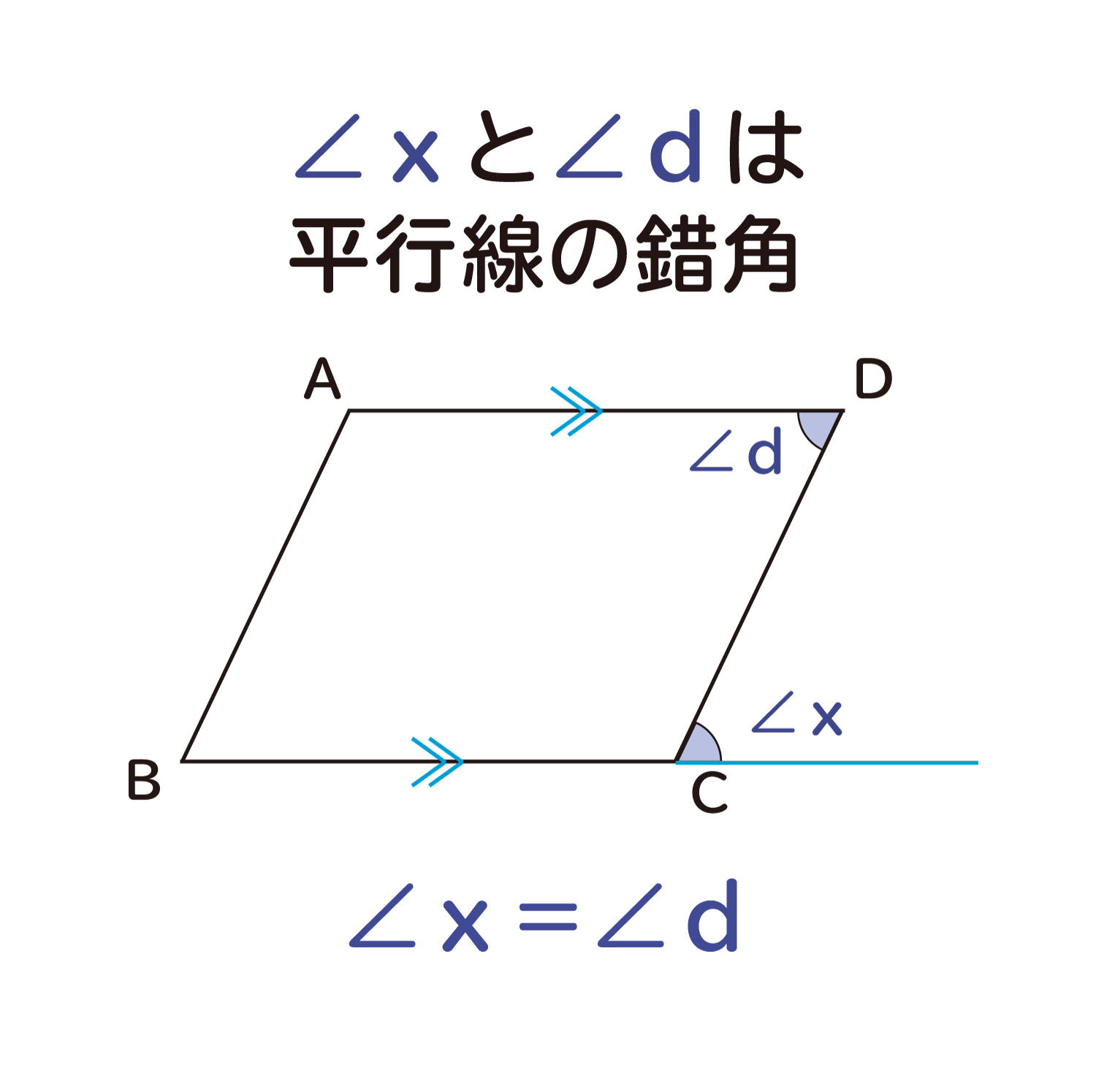



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル
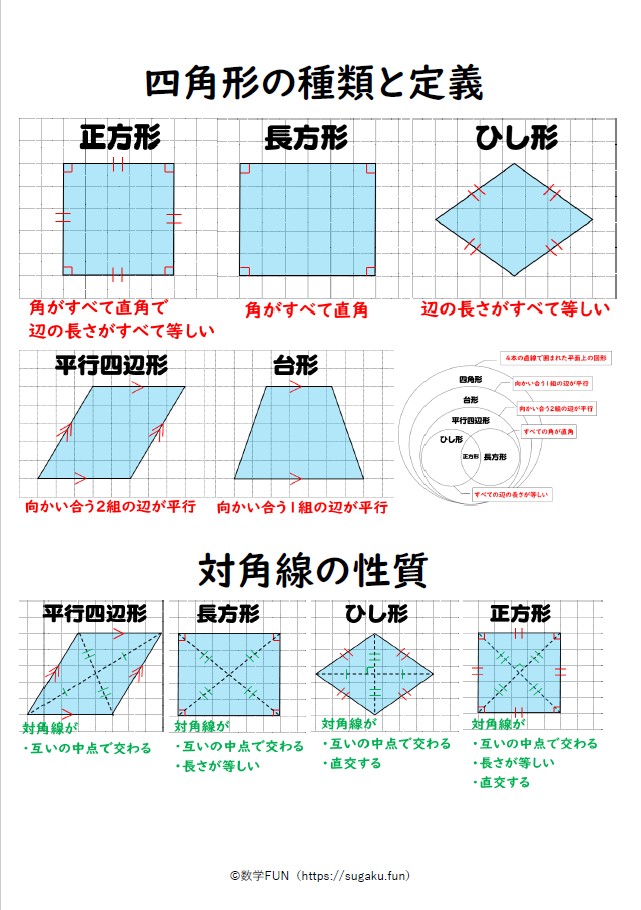



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の面積を対角線と角度から求める問題 Youtube
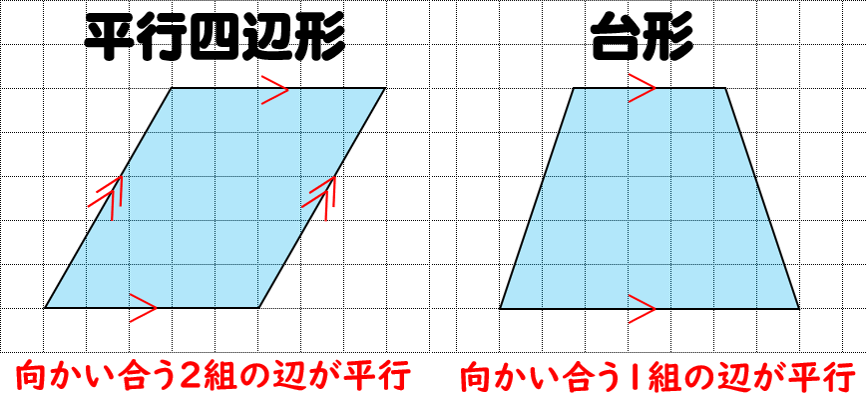



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形 対角線 長さ 計算
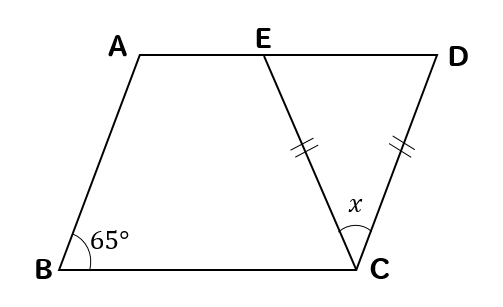



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




正方形 Wikipedia



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方




平行四辺形 対角線 長さ 計算




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形の辺や角を求める Youtube



画像のように 平行四辺形を対角線で切って出来る二つの三角形は 例外なく角 Yahoo 知恵袋
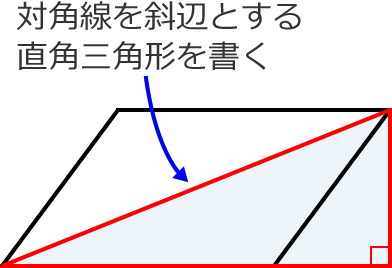



平行四辺形の対角線の長さの求め方




印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




パズルから数学へ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
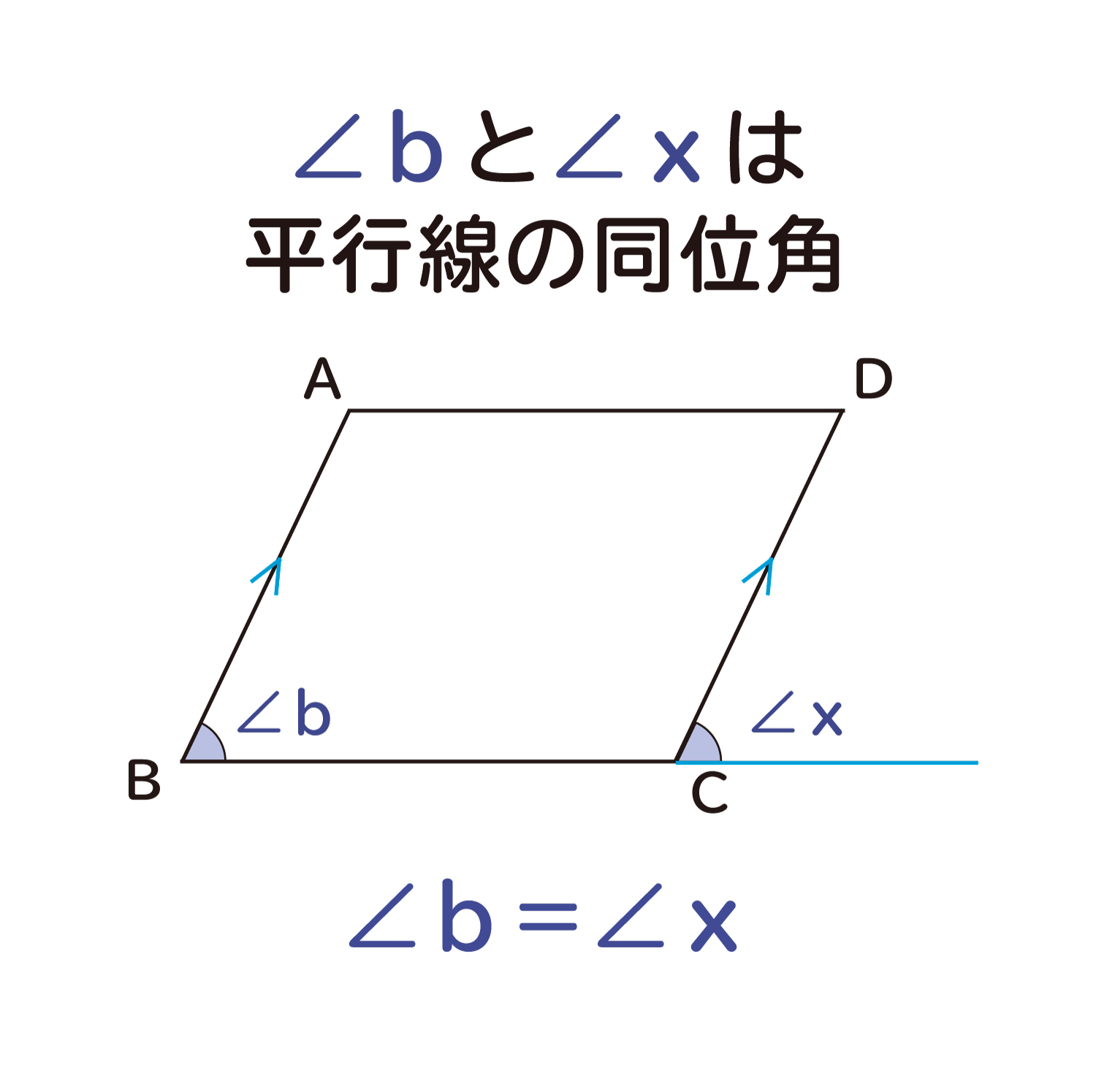



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1



1



1




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



0 件のコメント:
コメントを投稿