図形の証明問題は基本的に、三角形の合同条件などの「条件」を「根拠」を挙げて示す、というパターンです。 そのため慣れてしまえばワンパターンであるため得点しやすい問題ともいえます。ポイントを押さえて確実に得点したいところです。 わかったことを図に書き込んでおく! たいてい<前: L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答 :次> 練習問題1 以下の1~3に示した各組の三角形が相似であることを証明しなさい。 (※辺の長さの単位はcm) 1 ABCと EDC 2 ABCと AED 3 ABCと EBD 練習問題2 右図において、AD∥BCで、2つの線分ACとDB の交点をPとする。 このとき、 ADP ∽ C BPであることを証明しなさい。 練習問題3 右図に501中2・三角形と四角形・証明問題 01 学習塾学門 501中2・三角形と四角形・証明問題 01 21年11月6日 最終更新日時 21年11月21日 banno

等腰三角形 三角形的证明ppt 第2课时 下载 牛二ppt
中学生 三角形 証明 問題
中学生 三角形 証明 問題-三角形の合同条件を用いて証明するために,あと1つどのようなことが分かればよいですか。 下の = に分かればよいことを書きなさい。 ・分かっていること BC=EF ・分かればよいこと = D E F A B C 2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 練習問題② 2 次の問いに三角形の形状・証明問題 例 次の等式が成り立つとき,この ABCはどんな形の三角形か. a sin A=b sin sin C (答案) などを代入すると, これより,a2=b2+c2 ∠A=90゜の直角三角形・・・ (答) 最後の詰めは,どうするのか



中考数学 费马点 问题 王者再度归来
三角形の合同証明の総合的な練習問題です。 定期テスト対策や高校入試対策としてもご利用ください。 三角形の合同証明のポイント 基本的な合同条件、証明のやり方をしっかり確認してから取り組んでください。 三角形の合同 二等辺三 三角形の合同の証明応用問題の解答 ABEと ADCにおいて ABDは正三角形なので、AB=AD① ACEは正三角形なので、AE=AC① 正三角形の1つの内角は60°だから ∠EAB=60°∠BAC③ ∠CAD=60°∠BAC④ ③④より、∠EAB=∠CAD⑤ ①②⑤より そしたら、下のボタンを押してもう一度確認してみてください! 三角形の合同条件 ① 3組の辺が、それぞれ等しい。 ② 2組の辺とその間の角が、それぞれ等しい。 ③ 1組の辺とその両端の角が、それぞれ等しい。 直角三角形の合同条件 ④ 斜辺と1つの鋭角が、それぞれ等しい。 ⑤ 斜辺と他の1辺が、それぞれ等しい。 五つの合同条件に沿うものは見つけ
三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です. <原則>・・・角を辺に直す ⇒ ⇒ ⇒tanAは上記2つを用いて とします. B 証明問題①「相似な三角形を見つける」 証明問題① 下の図において、相似な三角形を記号を使って表しなさい。 また、そのときの相似条件も答えなさい。 どの相似条件を用いるかや、対応する頂点を合わせることに気をつけましょう。 解答 \(\triangle \mathrm{JKL}\) ∽ \(\triangle \mathrm{NMO}\) \(3\) 組出題範囲は違う(直角三角形」と「相似」)けど、ポイント・考え方はまったく同じ問題があります。 例題 $\textcolor{green}{1}$ (直角三角形) $\textcolor{green}{\rm BD = AE}$ であることを証明しなさい。 $\rm ABD$ と $\rm CACE$ において、
「中2の三角形と四角形の証明問題です。 テスト対策や入試対策に使って頂けると 嬉しいです\( ´˘`)/ 1/13ひし形まで更新済み 特別な平行四辺形まで更新したら 別ノートで演習問題とその解答をupする 予定です。 その際は関連ノートにリンクを貼ります。 p3~三角形の合同条件と証明 p14~二等辺三角形の証明 p21~正三角形の証明 p24~直角三角形の三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 A B C D E 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnとして、直線nと∠BCAの二等分線との交点をF,直線nと∠ACEの二等分線との交点をGとする。典型問題ですね。正答率も高め。 (2)(正答率%) 模範解答,図を見ると簡単そうですが,意外に難しい。普段から図に条件を書き込まない人はoutです。 ただ,普段から書き込んでいる人でも,結構迷います。どの三角形を証明するか。
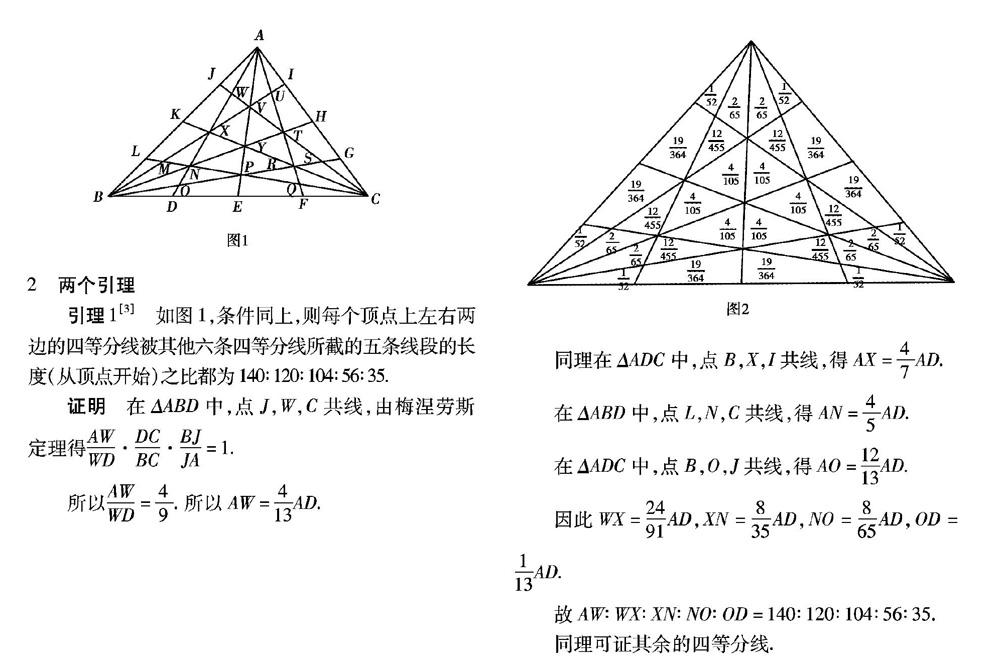



探究三角形四等分线分割面积的问题 参考网




知乎 有什么你认为很简单的问题实际的证明却很复杂 Mb5ff2f2755a961的技术博客 51cto博客
三角形の形状問題も,角度に関する式を辺に関する式に直してから考えるのが基本です. a=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90° の直角三角形 などど答えます. (単に「二等辺三角形」と答えると,どの2辺が等しいのか分かりませんので三角形の合同の証明 基本問題1 図でAC=DB, ∠ACB=∠DBCのとき, ABC≡ DCBを証明せよ。 A B C D 図でAB=DC, AC=DBのとき, ABC≡ DCBを証明せよ。 A B C D 右の図でAC//BD, AD//BCのとき, ABC≡ BADとなることを証明せよ。 A B C D 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト 平行と合同 要点 平行線の錯角と同位角 内角の和、外今回は三角形の相似条件や三角形の相似を証明する問題の解き方について見ていきましょう。 目次 相似な図形とは? 三角形の相似条件とは? 三角形の相似の証明問題 例題;




证明三角形为正三角形问题下载 Word模板 爱问共享资料



所有三角形都是等腰三角形 证明竟然无漏洞 问题出在哪里 每日头条
だけど、しっかりとした手順を身につけてもらえれば、すっごく簡単に解くことができるようになるよ! 今回の記事では、三角形の合同を証明する問題を基礎からみっちりと解説していくね! それでは、次の問題を利用して証明の書き方について解説していきます。 下の図で、AB=AD、BC=DCならば、 ABC≡ ADCとなることを証明し 直角三角形 1合同なることを証明する三角形を囲んでみましょう。 * ABCは正三角形 2仮定から、確実に等しい辺や角度に印を打ちましょう。 正三角形の辺、内角は等しい 3他に等しくなりそうな辺や角がないか考えます。 平行線の錯覚、対頂角などをまずは確認しましょう。 上の図で∠BAD=∠CBDが等しければ合同だと証明出来ます。 4角度を足したり 高校入試に出やすい証明問題①三角形の合同 まずは三角形の合同の証明です。基本問題から見ていきましょう。 例題 下の図でac=bd、ad=bcのとき abc≡ badとなることを証明せよ。 解答 abcと badにおいて abは共通 ac=bd (仮定) ad=bc (仮定) よって3組の辺がそれぞれ等しいので



1



头条问答 初中的相似三角形 中考怎么考 有什么好的解题技巧 孩子学习成长日记的回答 0赞
平行四辺形の対角線を証明する問題で、その対角線を含んでる三角形を選んで証明を進めたのですが、もう を選ぶところからが回答と違っていて。 2図形のなかの直角三角形は証明せずに、90度のマークをいれてもいいんでしょうか? また、証明しなければならないときはどのようにして 直角三角形の合同の証明問題について 中学2年です。 数学の学校の課題をやってて、一応だいたい解けるんですが、 「なんでそうなのか」がちょっとよくわかってないんで、 数学わかる方とかに質問です。藤村の三角形問題(ふじむらのさんかっけいもんだい、英 Kobon triangle problem )は離散幾何学の未解決問題で、藤村幸三郎により初めて述べられた。 この問題は、平面上に k 本の直線を引くときに重なり合わずに作ることのできる三角形の最大数 N(k) を求めるものである。



1



求三角形三边长问题 西瓜视频搜索
一般的な証明問題は「証明の型」と「考え方」が出来ると非常にラクなので、このページでシッカリと覚えていきましょう! 三角形の合同の証明 例題(1) 下の図で,∠ABC=∠DCB,∠ACB=∠DBCならばAB=DCとなること証明しなさい。 証明問題┃考える順番 証明の考え方の基本手順 (1)どの図形とどの図形の合同を証明するのか (2)使える材料をまとめる (3)どの合同条件を使うのか 角の大きさ (辺の長さ)は等しいので ( ∠ B D C =180°<一直線>より) ∠ A D B = ∠ A D C =90° = B D = C D となり 「二等辺三角形の 頂角の二等分線は底辺を垂直に二等分する」 を証明することができました これらの定理は 「証明の問題」以外でも 二等辺三角形 これにいくつか条件を加えて、証明する問題です。 一番よく見る形だと思います。 この問題は穴埋めよりも記述が多い印象があります。 この形だけでもいくつもの出され方があるので、しっかりと理解して解くようにしましょう。 一番基本の問題ですが、丸覚えが一番効か



等腰三角形证明 第1页 要无忧健康图库



面积问题 求三角形ced的面积 教育资讯 电影资讯网
直角三角形の合同証明の練習問題 次の図のように、bd=cdが等しく、∠abd=∠acd=90°の2つの三角形があるとき、∠adb=∠adcであることを証明せよ。 直角三角形の合同証明の解答 abdと acdにおいて 仮定より bd=cd① 仮定より、∠abd=∠acd=90°② 共通な辺より ad=ad③ ①②③より、直角 直角三角形解答の解答1 ABDと ACEにおいて 仮定より AB=AC① 仮定より ∠ADB=∠AEC=90°② 共通な角より ∠BAD=∠CAE③ ①②③より 直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、 ABD≡ ACE 合同な図形は対応する辺は等しいので、AD=AE スポンサーリンク証明入試問題 の2辺AB,ACをそれぞれ1辺とする正方形 ADEB,ACFGを ABCの外側につくる。 <問題2>右の図のように、1つの平面上に ることを証明しなさい。 がある。頂点Aから辺BCに垂線をひき、辺BCとの交 点をPとする。また、頂点Bから辺ACに垂線をひき、 辺ACとの交点をQとし、線分APと線



全等三角形学好全等三角形有诀窍学霸不用课本完全靠它 我有车




中考数学 三角形证明 题型总结 5
三角形と四角形 問題 z 二等辺三角形 z 二等辺三角形の性質 z 二等辺三角形であるための条件 z 正三角形 z 直角三角形の合同 z 直角三角形の合同条件を使った証明 z 平行四辺形 z 平行四辺形の性質 z 平行四辺形であるための条件 z いろいろな平行四辺形 z 平行線と面積 z 円周角 証明問題はパターンが少ないので、慣れれば実は簡単です。 覚えておくべき条件が少ない! 中学数学の証明問題をクリアするには、合同な三角形の性質以外に以下の性質・条件を覚えておけば十分です。 平行線の性質;17 三角形の合同の証明 132 復習問題 1 三角形の合同条件(2年) 次の図で,同じ印をつけた辺や角はそれぞれ等しい。 あてはまる合同条件を, それぞれ答えなさい。 ⑴ ⑵ ⑶ 次のことがらの仮定と結論を書きなさい。 ⑴ a=b ならば,ac=bc である。 ⑵ xが6の倍数ならば,xは3の倍数である。 ⑶ 長方形の1つの内角は 90ß である。 A B C D E F A B C D E F A B C D E F 1 「ならば」の前の部分 が




知乎 有什么你认为很简单的问题实际的证明却很复杂 凯特琳 博客园
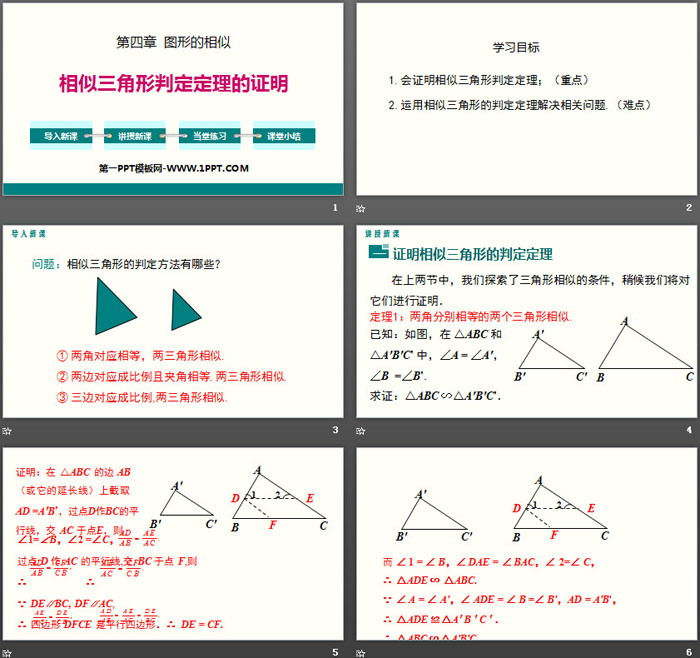



相似三角形判定定理的证明 图形的相似ppt 第一ppt
有名な問題です (1)に あるように 相似な三角形は「3つ」 あります 直角「90°」以外の 角に「 」と「×」の 印を入れると 見つけやすいと思いますよ 三角形の相似の証明のまとめ ・長方形の折り返し 一直線に「直角」が刺さった形 三角形の内角の和180° 一直線180° を利用して 同じ角を見つける ・平行の証明 「合同」と同じように 相似の証明 ↓ 対応する角は等しい ↓ 錯角が等直角三角形を利用して二等辺三角形であることを証明 証明問題の書き方を基礎から見直したい方は、まずこちらの記事を読んでみてくださいね (^^) 合同な三角形の証明問題の書き方を基礎から解説! それでは、順に解説していきます。 直角三角形の合同条件、証明についてはこちらの動画でも解説しているのでご参考ください^^この問題では、与えられた \(2\) つの三角形が合同であると証明せよ、というのです。ですので、「合同なのか合同ではないのかの判定」をするのではありません。合同なんです。合同である 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページ
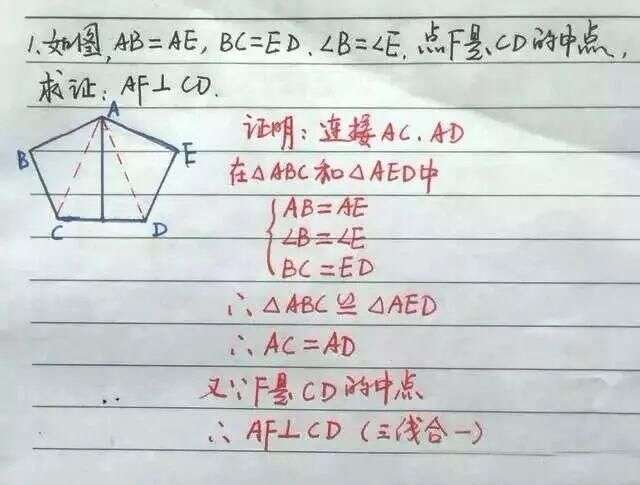



初中数学 证明三角形全等怎么添加辅助线 例题 讲解帮你搞懂 楠木轩



初中数学 证明复杂三角形全等的绝好思维方式 谁掌握谁受益
証明問題①「合同な三角形のペアを見つける」 証明問題① 次の図において、合同な三角形を記号を使って表しなさい。 また、そのときに使った合同条件も答えなさい。 どの合同条件を用いるかや、対応する頂点を合わせることに気をつけてくださいね。 解答 \(\color{red}{\triangle \mathrm{ABC} \equiv今回は三角形の合同条件や三角形の合同を証明する問題の解き方について見ていきましょう。 証明問題は今までの問題とは違った解答をしないといけないため戸惑うかもしれませんが、ポイントを解説しているのでぜひ参考にしてください。 目次 合同条件とは? 三角形の合同条件に関する練習問題3 右図の ABCと C DEは正三角形である。 このとき、AD=BEであることを証明しなさい。 練習問題4 右図の BADと BC Eは直角二等辺三角形で、点A,B,Cは同じ直線上にある。 このとき、AE=C Dであることを証明しなさい。 練習問題5 右図の ABC は∠AC B=90°の直角三角形である。 AEは∠BAC の二等分線であり、またAB⊥C Dで、AEとC Dの交点をPとする。 このとき、



非常全面的中考数学经典题型 三角形综合 看完能把这类题解透 每日头条



等腰直角三角形
相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です 図形と角、三角形、四角形 図形と角、三角形、四角形② 図形と角、三角形、四角形、場合の数 テストで90点以上が取れるコツ 定期テスト過去問を解くだけでも、十分な得点を狙えます。 しかし、満点を狙いたい方へ。




相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt




思维问题 1 用一根铅笔证明三角形内角和




中考数学 三角形证明 题型总结 3



初中几何三角形考法大全 小初高题库试卷课件教案网




等腰三角形 三角形的证明ppt 第2课时 下载 牛二ppt



等腰三角形 第1课时 我的网站
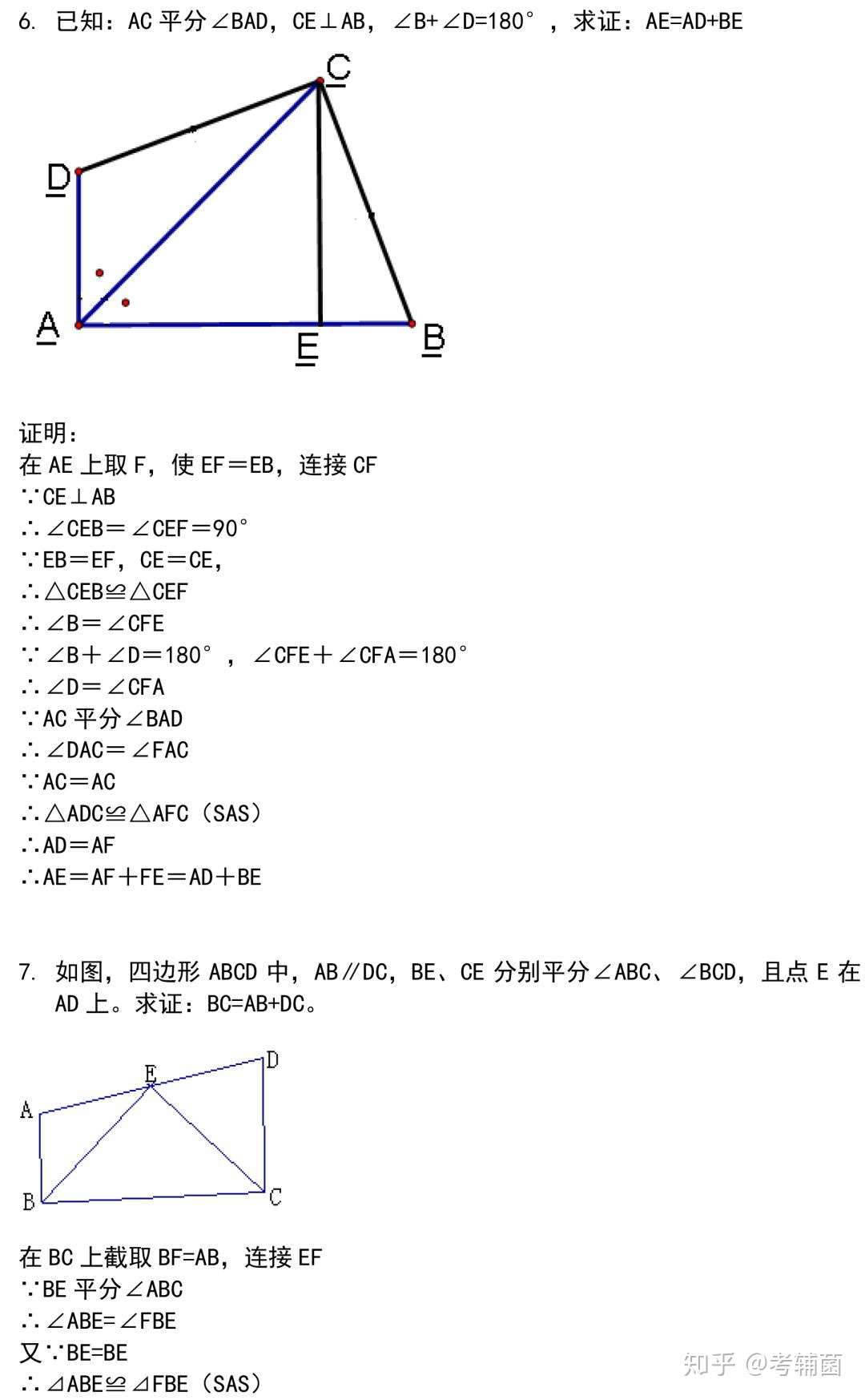



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 知乎



头条问答 初二数学难点在哪 三角形那章应该注意什么 用户的回答 0赞



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分




快乐数学 惊天大秘密 所有三角形都是等腰三角形吗 你能发现问题吗 哔哩哔哩




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




等腰三角形 三角形的证明ppt 第2课时 下载 牛二ppt




等腰三角形 三角形的证明ppt 第2课时 下载 牛二ppt




合同の証明 清水塾




年中考数学必考考点压轴题 等腰 等边三角形问题 初中数学知识点 哔哩哔哩




平面几何 相似证明角度相等问题 哔哩哔哩



动点定角问题 证明垂直 正方形 箭型全等 直角三角形斜边上的中线 哔哩哔哩 Bilibili



全等三角形证明方法归纳 典例详解几种辅助线做法 含思路分析 电竞主播网




知乎 有什么你认为很简单的问题实际的证明却很复杂 凯特琳 博客园




相似三角形 几何证明问题中关于比例线段的分析策略探究 启示号




如何逐步进行几何证明 科学 22




三角形中三条高共点问题 参考网



等边三角形存在性 西瓜视频搜索



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 几何




三角形重心証明 Ronia
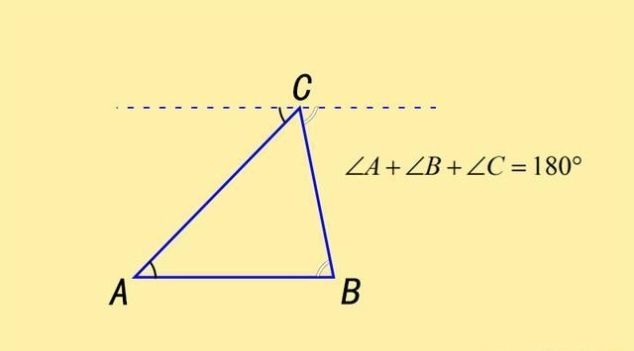



三角形内角和为180度 这个问题数学家研究了两千多年 快资讯
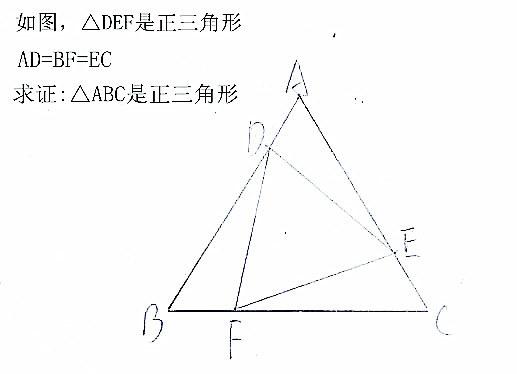



如何证明这个看似结论显然却难以证明的平面几何命题 知乎



七年级数学几何难题练习题 含答案 腾讯新闻



中考数学考点44 以三角形为基础的图形的旋转变换问题 小初高题库试卷课件教案网



查看答案



七年级数学几何难题练习题 含答案 小初高题库试卷课件教案网



全等三角形学好全等三角形有诀窍学霸不用课本完全靠它 我有车



利用费马点的性质证明拿破伦定理 确实够烧脑 托里拆利 费马 三角形 新浪新闻




初中数学 证明线段不等关系或最值问题常用思想方法原理与技巧 三角形 垂线 矩形 网易订阅



金磊 解题研究 三角形三条高线共点的十种证明 初中数学 腾讯新闻




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




平面几何 一大类角格点问题的统一证明 百度经验



全等三角形的证明过程 西瓜视频搜索




精華 初中數學八大題型點撥 四 開放探究問題 雪花新聞




平面几何 赛瓦定理证明三角形的三条垂线或中线或角平分线三线共点问题 Linux 0 11调试教程 程序员its404 证明三角形三条角平分线共点




几何相似定律在电机中的应用 皖南电机




二等辺三角形の性質と証明 無料で使える中学学習プリント




三角形全等的判定定理证明过程
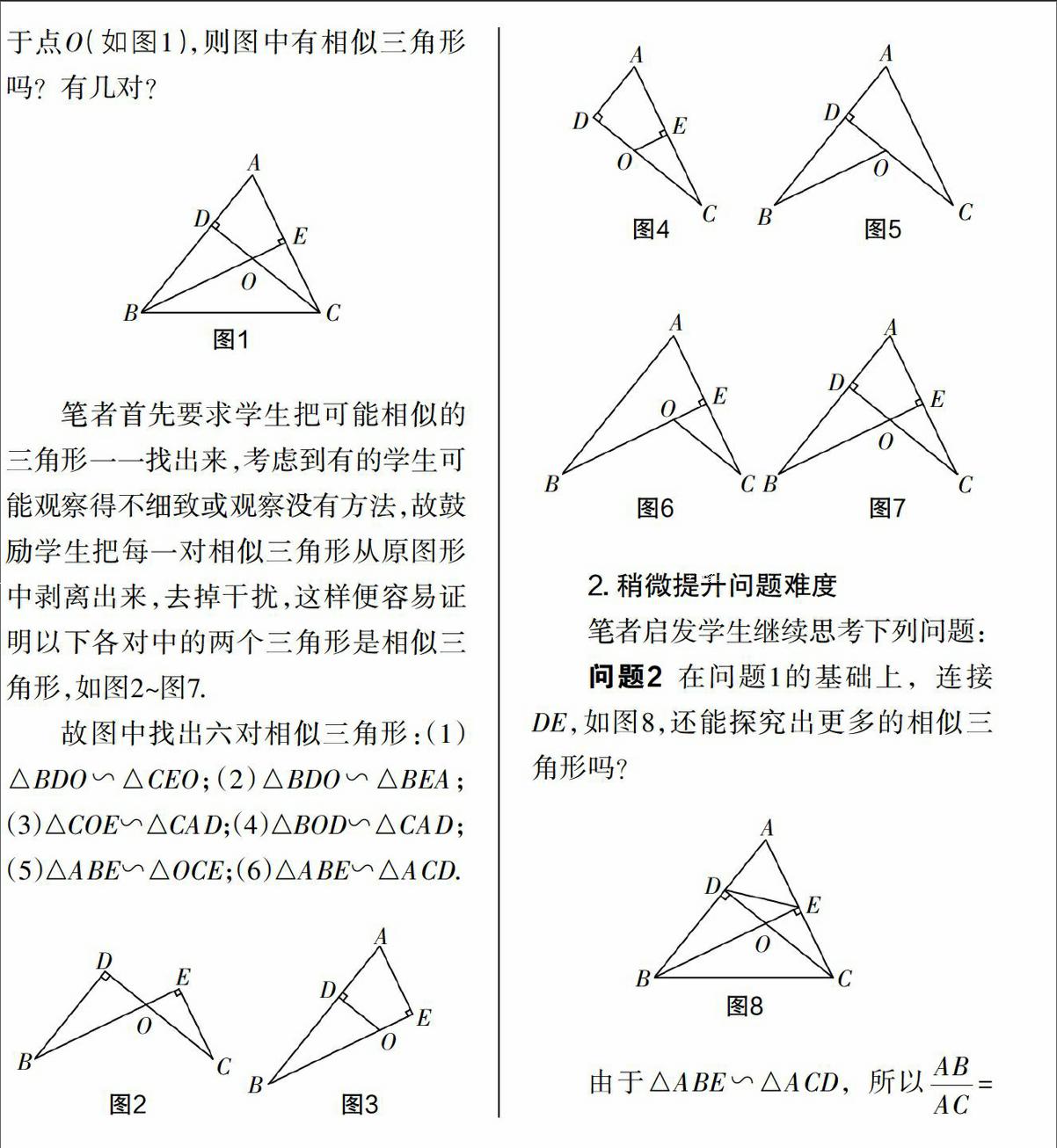



三角形中三条高共点问题 参考网



中考数学 费马点 问题 王者再度归来



初中三角形中线定理证明三角形中线定理的定理证明 朵拉利品网



三角形180度证明方法 西瓜视频搜索



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 几何



一个和九点圆心相关的证明共线问题 Geogebra 22 01 22 29 23 哔哩哔哩 つロ干杯 Bilibili



Ssa证明三角形全等 西瓜视频搜索



难题文章 难题问题还有什么题 招生信息网



角平分线定理证明 西瓜视频搜索




浅谈辅助线在全等三角形证明中的应用 参考网



利用基本图形证明三角形相似 中国期刊网




现货包邮哈工大steiner问题 分角线相等的三角形 初等几何机器证明问题精装吴文俊 摘要书评试读 京东图书




第16讲等腰三角形 暑假辅导班 21年新八年级数学暑假精品课程 华师大版 Zip 师客文库



构造等腰三角形 证明几何问题 杂志论文 理科考试研究
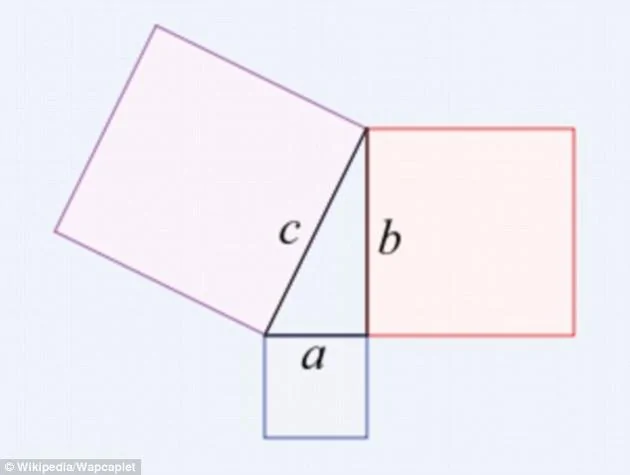



最长数学证明破解世界难题 全部阅读需100亿年 阿波罗新闻网



初一数学几何技巧 如何快速找全等三角形 雪花新闻




中考数学 三角形证明 题型总结 9




巧借等腰直角 等边三角形特性添加辅助线 多源焦点



巧用向量的加法证明点线问题 科学猫




等腰三角形 三角形的证明ppt 第4课时 第一ppt



七年级数学几何难题练习题 含答案 小初高题库试卷课件教案网
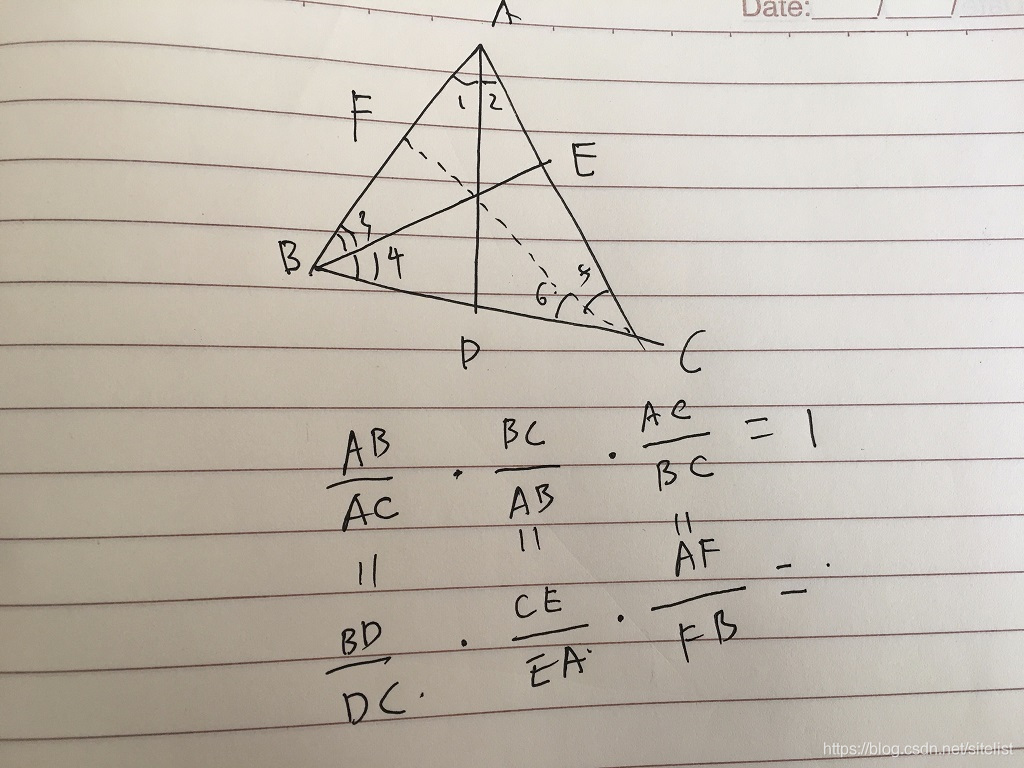



平面几何 赛瓦定理证明三角形的三条垂线或中线或角平分线三线共点问题 Linux 0 11调试教程 程序员its404 证明三角形三条角平分线共点
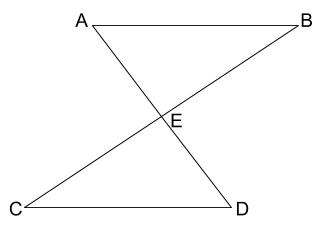



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su




相似三角形的判定和性质 初中数学知识点总结 星火网校




浅谈辅助线在全等三角形证明中的应用 参考网




中考数学 三角形证明 题型总结




等腰三角形 三角形的证明ppt 第4课时 下载 牛二ppt



1




中考数学 三角形证明 题型总结 4




几何三角形证明题 初三数学 三角形证明题 三人行教育网 Www 3rxing Org



中考数学考点44 以三角形为基础的图形的旋转变换问题 小初高题库试卷课件教案网
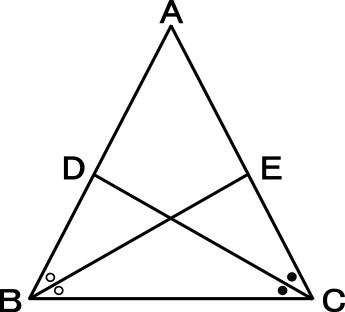



中学2年数学練習問題 図形と合同 三角形の合同の証明問題
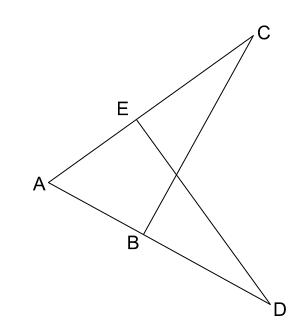



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su




三角形の合同証明の練習 無料で使える中学学習プリント



六招 辅助线解决全等三角形证明问题研究 参考网



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




思维问题 1 用一根铅笔证明三角形内角和




母子型 相似模型的解读与应用探究 参考网




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット
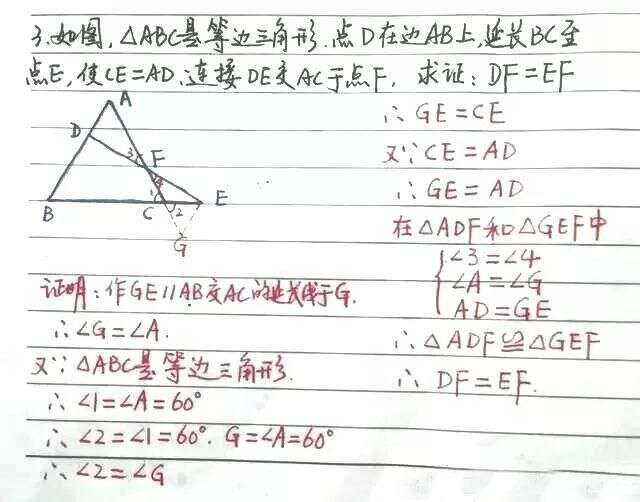



初中数学 证明三角形全等怎么添加辅助线 例题 讲解帮你搞懂 楠木轩



构造等腰三角形 证明几何问题 杂志论文 理科考试研究




等腰三角形 三角形的证明ppt 第4课时 下载 牛二ppt




专题17 等腰 等边三角形问题 原卷版 Docx 师客文库



0 件のコメント:
コメントを投稿