
合同式の性質を使った整数の余りの計算方法 趣味の大学数学
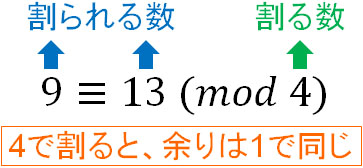
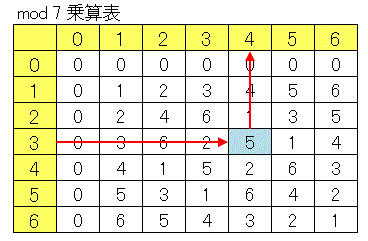
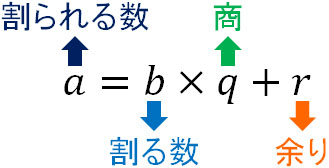
簡単な合同方程式の解き方 合同式の基本的性質 (11) 反射律 (証明) だから, と は を法として合同であると言える. (12) 対称律 ならば (証明) ならば だから成り立つ. (13) 推移律 かつ ならば (証明) ならば だから成り立つ 合同式の四則計算 (1) かつ ならば (21) (22) (23) (証明) かつ ならば (21) だから, が成り立つ. (22) だから, が成り立つ. (23) だから, が成り立つ. ※ 合同式の表記 27≡2≡-3(mod 5) 7で割った余りを求めたいわけですが、注目しないといけないのは $1\cdot2\cdot3\cdot4$ だけです。 から7の倍数を捨てたわけですが、 展開する前に捨ててしまってもかまわない というのが合同式の基本的な考え方
合同式 解き方 x二乗
合同式 解き方 x二乗- 今回は一次合同式の解き方について解説しました。 ポイントはの係数が1になるように、2つの式を連立させることです。 一次合同式にはもっと面倒なタイプもありますが、大学入試や数学検定1級のレベルであれば、今回のタイプを学んでおけば十分だと思います。 実際に、数学検定1級でよく出題される、連立合同式も今回ご紹介した解法を組み合わせていくだけです。 次の本では1次 合同式の基本的な性質 合同式に関して次の基本的性質が成り立ちます. m m を整数とする. a ≡ b, c ≡ d (mod m) a ≡ b, c ≡ d ( m o d m) のとき,次が成り立つ. ( 1 1 ) ac ≡ bd (mod m) a c ≡ b d ( m o d m) ( 2 2 ) a−c ≡ b−d (mod m) a − c ≡ b − d ( m o d m) ( 3 3 ) ac ≡ bd (mod m) a c ≡ b d ( m o d m) ( 4 4 ) an ≡ bn (mod m) a n ≡ b n ( m o d m) ( n n は自然数)

数a 合同式modと割り算の余り Youtube
というのが一番やるべきことなわけで、いかにも出て来るやつらと言えば、 ・行列 ・整数(合同式とかも) ・ベクトル(内積外積とか面からの距離とか) ・指数対数 ・確率 ・微積(微分方程式、重積分とかも) あたりだが、行列の単純計算とか固有方程式使って固有値出すとかはだいぶ慣れた 合同式を利用した解き方では、 法に定めた数で割ったときの余り に注目して解いていきます。 上手に利用できれば、式変形や面倒な計算がないので、とても有効な解き方です。 合同法を利用して不定方程式の一般解を求める手順は以下のようになります。 合同法を利用して不定方程式の一般解を求める手順 方程式 a x ± b y = c ( a > b) から合同式 a x ± b y ≡ c ( mod b) へ置き換える。 と言う人は、 合同式(基本編)基本的な問題で合同式を使う練習 合同式を使いこなすことで、整数分野の問題(余りに関する問題)を簡略化して処理できる。 しかし慣れが必要であるため、基本的な問題を用いて合同式に慣れるための演習問題。 13の100
合同式まとめ:巨大な数をどんどん小さい数へ ということが、この類の問題を解く時に一番大切です。 そして、その過程で底となる数(今回は2)の何乗かが、法の数の倍数と比べた時(5の倍数) ±1や0等簡単な数字になるように うまく"べき乗"を作ってやる とうまく解くことが出来ます。 この様にして、普通では計算できない様な数を扱える事が合同式の最大の強みと言えます n_1,n_2 n1,n2 と n_3=5 n3 = 5 も互いに素だったので、さらにひとつの合同式にまとめられて、結果としてすべての合同式を満たす解が見つかるわけです。 この連立合同式の解き方を一般化したものが、 中国式剰余定理 (Chinese remainder theorem)です。 a_1,a_2,\dots,a_r 合同式に慣れていない場合は、この方法がおすすめです! おすすめ2 合同式を使う方法 一番スマートな方法です。 合同式の式変形に慣れている場合は、この方法がおすすめです! 特殊解だけでなく、直接整数解を求めることが可能なのでとても便利です。
合同式 解き方 x二乗のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 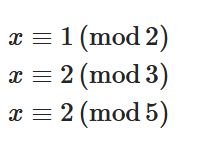 |
 |  |  |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | .png) |  |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 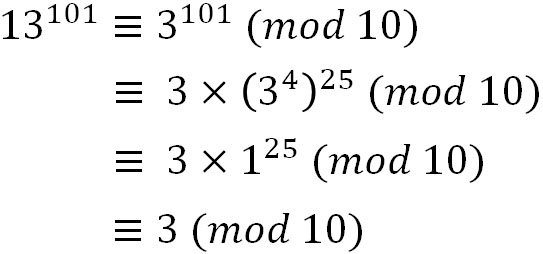 | |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 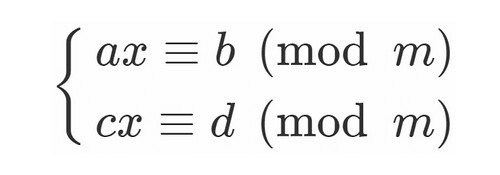 |
 |  |  |
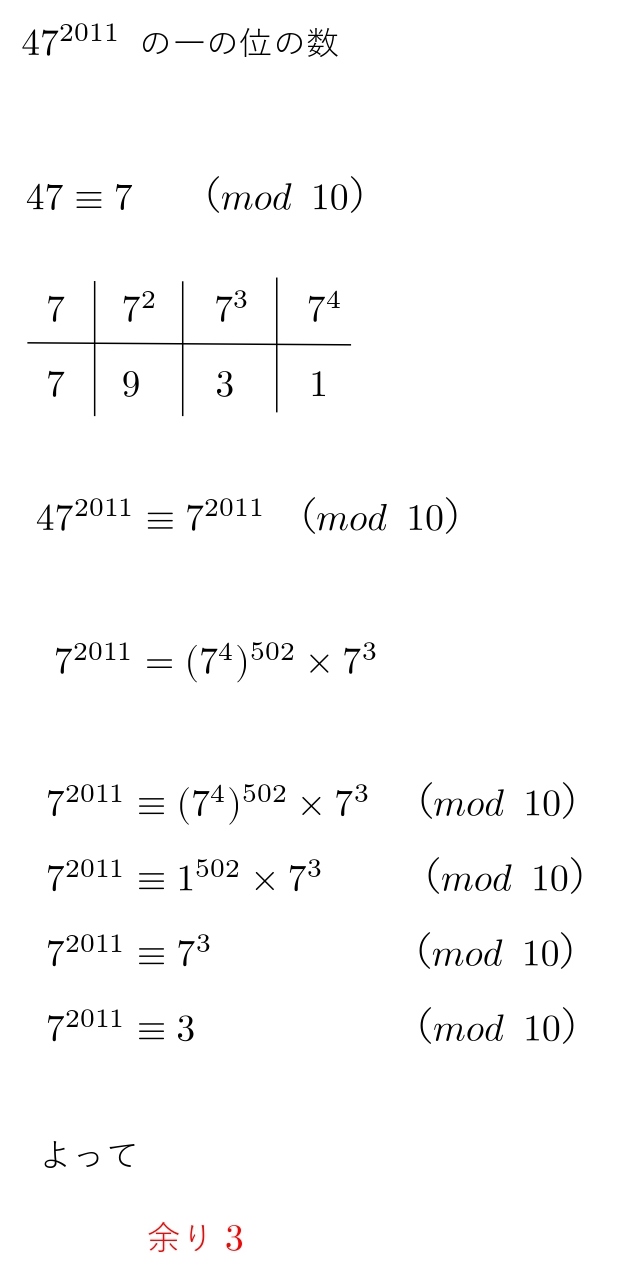 |  |  |
「合同式 解き方 x二乗」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
つまり合同式として正しい式は無限に書けます. 例 −13 − 13 を 17 17 で割ると −1 − 1 余り 4 4 なので −13 ≡ 4 − 13 ≡ 4 ( mod 17 ( mod 17 ) と書けます. a a や商がマイナスでも構いません. 合同式の性質 ポイント 合同式の性質 a ≡ b a ≡ b (mod m ( mod m ), c ≡ d c ≡ d (mod m ( mod m )のとき以下のように 加減乗 が成り立つ. 加法 a c ≡ bd a c ≡ b d (mod m ( mod m ) 減法 a− c ≡ b−d a − c例題 合同式を使って、整数方程式を求めていきましょう。 x とy は整数とします。 この問題も x とy に当てはまる整数が思いつけば簡単ですが、そうでない場合はユーク リッドの互除法を使うという手もあります。しかし、ここは合同式を使いましょう。変
Incoming Term: 合同式 解き方, 合同式 解き方 累乗, 合同式 解き方 x二乗, 合同式 解き方 方程式,




0 件のコメント:
コメントを投稿