今回のポケモン解説はマルマインです。 目次 基本データ 進化 図鑑説明 耐性 容姿 概要 ゲームのマルマイン トラップ役 対戦のマルマイン 能力 特性 オススメ技 特殊技 物理技 変化技 テンプレート型 対マルマイン 注意すべき点 対策方法 戦法 第五世代 第七世代 『大乱闘スマッシュブラザーズ
Josspixmtla
[無料ダウンロード! √] ��体地図 作り方 小学生 222193-立体地図 作り方 小学生
まず地図で製作したい範囲を決める。 広くすれば当然作業量は増えるのであまり欲張らないのが大事。 限られた大きさで山の数や有名ポイントが入るように工夫する。 図を拡大コピーしただんだん地図の作り方・更に快適に作るには? 石膏で仕上げた立体地形模型です。 この道30年のベテラン職人が精密に等高線を再現した、コンタ (等高線)模型です。 すべて手作りですので100商模型に地図を貼り付ける例 材料色の3Dプリンタで出力した立体模型に、 VRMLのダウンロードフォルダに含まれる画像ファイル「texturepng」の紙プリントを貼り合わせました。 作り方を紹介

地形図から立体模型を作る 中学 Nhk For School
立体地図 作り方 小学生
中 1 理科 中学 理科 教科書 241302-理科 教科書 小学校 ���校図書
教授用資料 機関誌「中学校教育フォーラム」やポスターなどのダウンロード資料 教師用指導書 「理科の世界」教師用指導書のご案内 問題集 中学校理科の教科書準拠問題集「学習サポート」と 単元 身のまわりの物質とその性質,気体の性質,物質のすがたと状態変化,水溶液の性質, 学年 中学1年生 勉強ノート公開サービス。 30万冊を超える大学生、高校生、中学生のノートをみお問い合わせ先 生産物流部 拡大教科書担当係 住所 〒大阪府大阪市天王寺区大道4丁目3番25号 啓林館 生産物流部 拡大教科書担当係 TEL 06 6775 6541(生産物流部教科書担当直

中学理科 教科書 問題集セット メルカリ
理科 教科書 小学校 学校図書
桜えび 生しらす 静岡 799040-桜えび 生しらす 静岡

送料無料 釜揚げ桜えび しらすセット 化粧箱入り 敬老の日 塩辛と静岡の味 駿河屋賀兵衛 プレゼント ギフトのギフトモール
Web 静岡の桜えび10選! ここでしか食べられないおすすめの味 出典: 我武者羅ダディさん 静岡の桜えび10選! ここでしか食べられないおすすめの味 駿河湾に面し富士山の恵Web楽天市場「静岡 生しらす 生桜えび」106件 人気の商品を価格比較・ランキング・レビュー・口コミで検討できます。ご購入でポイント取得がお得。セール商品・送料無料商品も多数。「
桜えび 生しらす 静岡
200以上 ポケモン ファイア���ッド ピカチュウ 103874-ポ���モン ファイアレッド ピ��チュウ
ファイアレッド Twitter Search Twitter
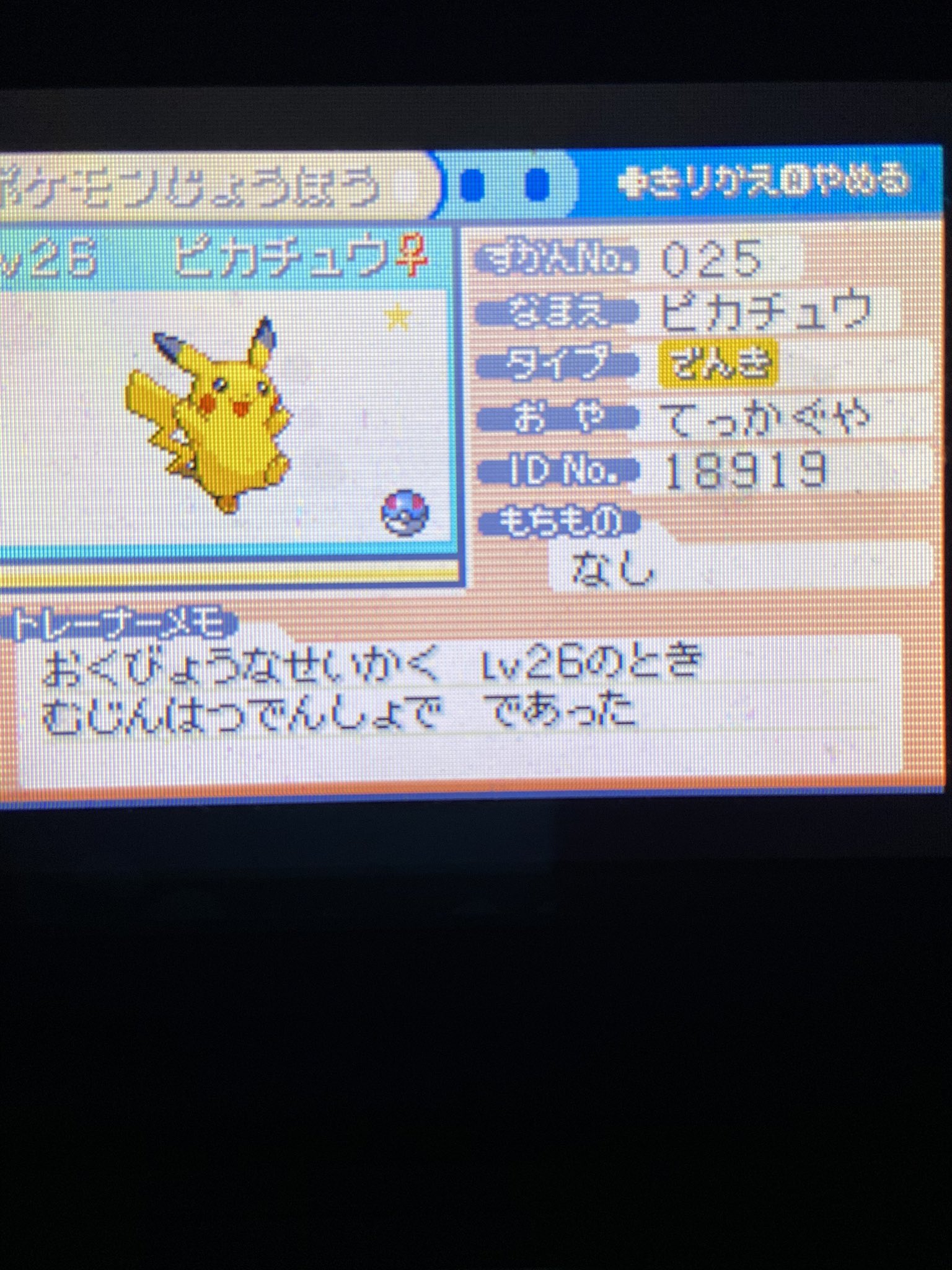
ポケットモンスターシリーズ 価格 5,040円 / 4,800円(価格改定後) 対応ディバイス ゲームボーイ対応リモコン 発売日 04年1月29日 『 ポケットモンスター ファイアレッド 』、『 ポケットモピカチュウ の種族値、タイプ相性、入手方法、進化方法、レベル技、教え技、タマゴ技、技マシン、秘伝マシンなどを掲載。 ポケットモンスター ルビー・サファイア・エメラルド(ポケモンRSE)
ポケモン ファイアレッド ピカチュウ
[最も共有された! √] ア��ア 国 首都 地図 358489-アジア 国 首都 地図
6 hours ago アジア幸福指数1位、「この国」の秘訣は (ハンギョレ新聞) Yahoo!ニュース 1 2 台湾の首都台北の様子。 台湾はここ数年間、幸福指数でアジアOpen full screen to view more This map was created by a user Learn how to create your own問2 地図中の2~15の国名と首都名を書いてみよう。 国名 首都名 1 日本国 トウキョウ 2 3 4 5 6 7 8 9 10 11 12 13 14 15 「西アジアと北アフリカの国々と首都」 課題 7 地図を見て、問1、問2をやってみよう。 解決する手がかり:教科書P34~47 P64~67 地図帳:P1~3 P158~160 問1 次の空欄に国名や地名を書きこもう。
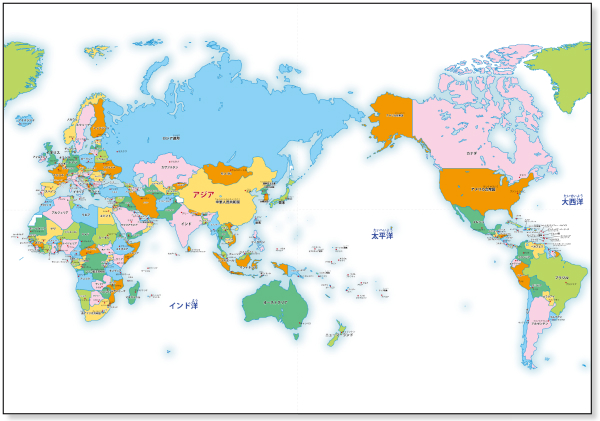
子ども用 世界地図 カラー 国名 首都名 無料ダウンロード 印刷 ちびむすドリル 小学生
アジア 国 首都 地図
[新しいコレクション] 合同 式 解き方 251291-合同式 解���方 x二乗

合同式の性質を使った整数の余りの計算方法 趣味の大学数学
簡単な合同方程式の解き方 合同式の基本的性質 (11) 反射律 (証明) だから, と は を法として合同であると言える. (12) 対称律 ならば (証明) ならば だから成り立つ. (13) 推移律 かつ ならば (証明) ならば だから成り立つ 合同式の四則計算 (1) かつ ならば (21) (22) (23) (証明) かつ ならば (21) だから, が成り立つ. (22) だから, が成り立つ. (23) だから, が成り立つ. ※ 合同式の表記 27≡2≡-3(mod 5) 7で割った余りを求めたいわけですが、注目しないといけないのは $1\cdot2\cdot3\cdot4$ だけです。 から7の倍数を捨てたわけですが、 展開する前に捨ててしまってもかまわない というのが合同式の基本的な考え方
